Mehmet S. Mutluer
Sıkının namluyu terk ettikten sonra hedefe varıncaya kadar olan olayları “dış balistik” olarak tanımlamıştım. Genellikle saçma atmak üzere tasarlanmış yivsiz tüfeklerle yakın sayılabilecek mesafelerde orta ve büyük avlara veya hedef atıcılığında yivsiz tek kurşunlar da kullanılmaktadır. Saçma balistiğini farklılıkları nedeniyle başka bir sayfada aktarmaya çalışacağım. Aslında okuyucularımızın bildiği konular.
Yivsiz tek kurşunlar, yivlilere göre hızı az, menzili düşük, isabet oranı düşük mermilerdir.
Nedenlerini kabaca şöyle sıralayabiliriz:
- Namlu çıkış hızları yivlilere göre çok düşüktür.
- Cüsseleri yivli mermilerden fazladır, dolayısı ile sürüklenme katsayıları yüksektir, hava direnci ile kısa mesafede hız kaybederek düşmeye başlarlar
- Çoğunlukla künt uçlu olduğundan aerodinamik yapıları yivlilere göre kötü ve Balistik katsayıları oldukça düşüktür
- Yivli mermiler gibi jiroskobik dengeleri yoktur (veya çok az), daha çok çekme (sürüklenme) dengesi ile hareket ederler
- Üzerleri kaplı olmadığından namlu sürtünmesinden dolayı ısınma ile şekilleri kolay bozulur, aerodinamik yapıları daha namludan çıkmadan bozulabilir
- Transsonik bölgeye kısa mesafede girerler, denge ve seyirleri çabuk bozulur
Yivsiz tek kurşun barut gazlarının basıncı ile namlu ağzından bir ivme ile fırlatıldıktan sonra, içinde seyrettiği ortamın (hava) direnci ve sürtünmesi ile giderek hız kaybederken, ağırlığına bağlı olarak yer çekimi etkisi ile düşmeye başlarlar.
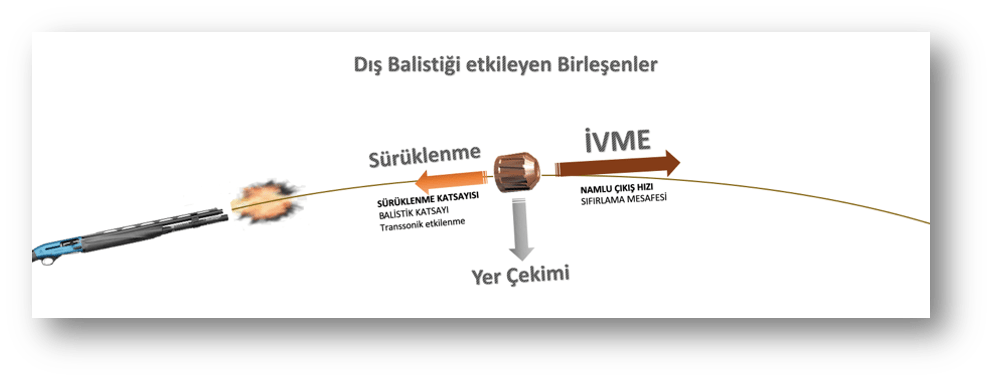
Yukarıdaki resimde bir mermi çekirdeğini etkileyen birleşenler görülüyor.
Namlu çıkış hızı ve Sıfırlama mesafesi
Eğer bir mermi, uzay boşluğunda hava direnci ve yer çekimi olmaksızın atılsa, sonsuza kadar ayni doğrultuda seyredecektir. Hava direnci olmadan, sadece yer çekimi etkili olsaydı, parabolik bir yörünge izlerdi:
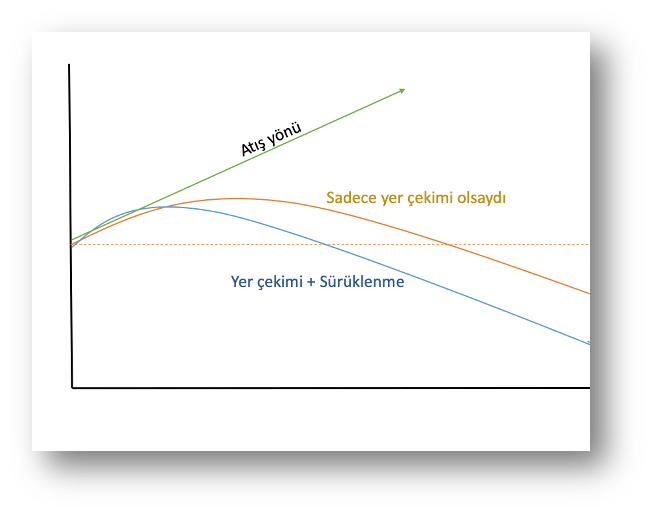
Oysaki hem yer çekimi etkisi, hem de içinde seyrettiği hava direnci ve sürtünmesi ile birlikte daha çabuk hız kaybederek, daha erken düşmeye başlar.
Atış esnasında atış hattı ile namlu doğrultusu paralel gibi görünebilir. Böyle olsaydı şekilde görüleceği gibi mermi 10-15 metre sonra gerek sürüklenme, gerekse yerçekimi etkisi ile düşmeye başlardı. Aslında gez, arpacığa göre (sıfırlama mesafesine bağlı olarak) çok az yüksektir.
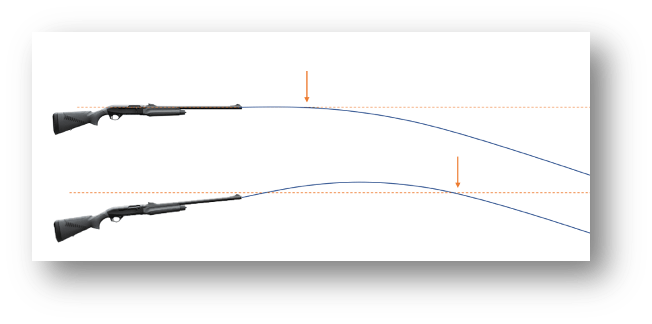
Namlu hattı ile atış hattı arasında (sıfırlama mesafesine bağlı) 0,04 – 1,5 derece arasında bir açı vardır. Bu açı nedeniyle mermi namludan çıktıktan sonra nişan hattına doğru yükselir, namlu çıkış hızına bağlı olarak 10-15 metre sonra nişan hattını keser, bir miktar yükseldikten sonra sürüklenme ve yer çekimi etkisi ile sıfırlama mesafesinde nişan hattını ikinci kez keserek düşmeye başlar.

Sıfırlama mesafesi, saçma atan tüfekler için genellikle 40 yarda (36,5 m) dir. Yivsiz tek kurşunlar için 25-50-75-100 metreler (veya yarda) için sıfırlama yapılır.
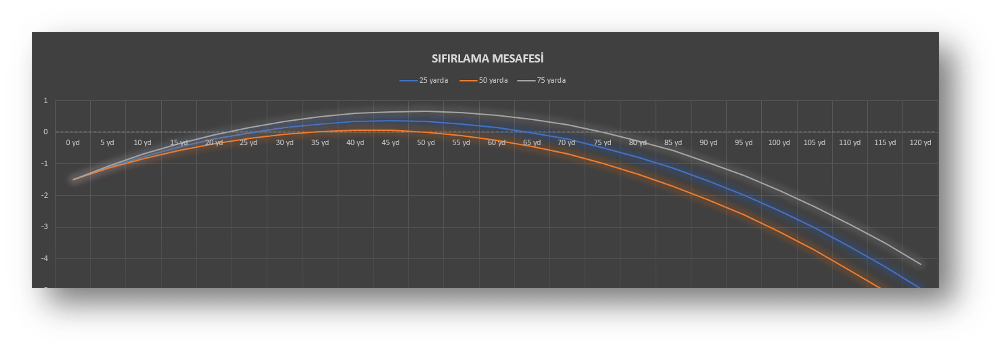
Bu grafik 100 yarda için sıfırlanmış bir tüfekte 32 gram Foster tipi çekirdek için düzenlenmiştir. Bu grafikteki mermi yolu üzerine konmuş biçimi işaretler o hızda çekirdeğin girdiği transsonik bölgeyi göstermektedir (Konunun içinde anlatılacaktır). Namlu çıkış hızı arttıkça transsonik bölgeye girme gecikmekte ve isabet artmaktadır.
Sürüklenme (Drag)
Bir cismin akışkan bir ortamda hareketi esnasında hareketini engelleyen dirence sürüklenme (drag) denmektedir. Bu hava içerisinde olursa aerodinamik sürüklenme veya hava direnci denmektedir.
Yivsiz tek kurşunlar künt uçları ve daha geniş çapları nedeniyle, yivli kurşunlara göre daha fazla hava direnci ve sürtünmeye maruz kalırlar. Bu nedenle daha çabuk hız ve dolayısıyla irtifa kaybederler.
Biraz fizik yönüyle inceleyelim. Alan (A) başına düşen güç (F) bize basıncı (P) verir, formüle dökersek:
P= F/A , buradan gücü hesaplarsak F=P.A olur. Burada gücü sürüklenme (Fd) olarak alırsak alırsak ve basıncı da Bernoulli denkleminden alırsak Fd= (1/2 r v2 ) A gibi bir denklem ortaya çıkar. (r = havanın direnci, v2 hızın karesi) . Bu formülü sürüklenme için yeniden düzenlersek:
Fd= ½ r v2 Cd A
Burada Cd nereden çıktı derseniz o da “Sürüklenme katsayısı” dır. Sürüklenme katsayısı Reynold sayılarına da bağlı boyutsuz bir sayıdır. Sürüklenme katsayısı hava içinde hareket eden cismin karşılaşacağı direnci ifade eder:
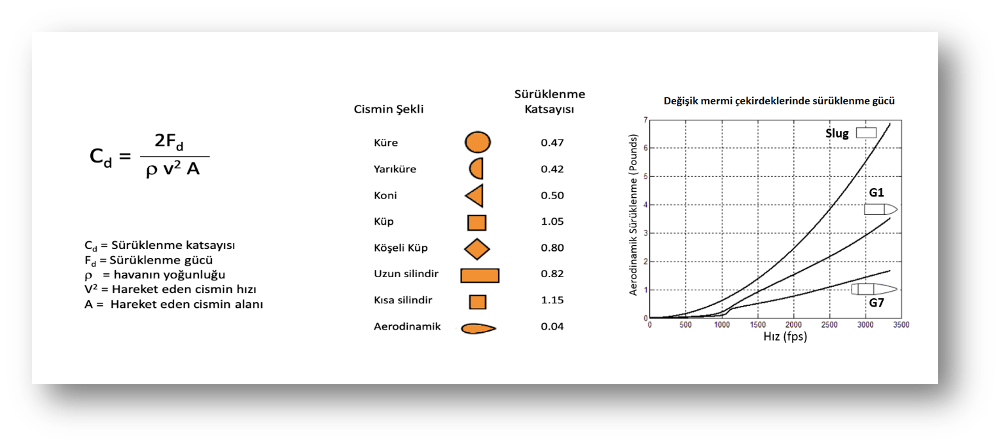
Cismin sürüklenme katsayısı ne kadar küçükse, havada seyri esnasında karşılaşacağı direnç o kadar az olacaktır. Örneğin tapasıyla seyreden tek kurşunlar (uzun silindir), tapasız seyredenlere (kısa silindir) göre daha az hava direnci ile karşılaşır. Yivsiz tek kurşunlar, daha aerodinamik yapıya sahip G1 ve G7 formundaki yivli kurşunlara göre daha fazla sürüklenme gücüne maruz kalırlar.
Balistik Katsayı (BC)
Sürüklenme katsayısı mermi çekirdeğinin ne kadar hava direncine maruz kaldığını gösterirken, balistik katsayı (BC=Balistic Coefficient) o çekirdeğin hava direncini yenebilme yeteneğini gösteren katsayıdır. Balistik katsayı mermi çekirdeğinin, boyu, çapı, ağırlığı ve uç tasarımının hava direncine karşı hız, menzil ve dengeyi korumasını sağlayan bir katsayıdır, mermi tipine göre değişir. Yivli mermilerde özellikle uzun mesafe atışlarında önem taşır. Sürüklenme katsayısının tersine balistik katsayı ne kadar büyük olursa hızını daha iyi korur, rüzgardan daha a etkilenir, daha geç düşer ve isabet oranı artar. Balistik katsayı değişik yöntemlerle hesaplanabilir:

Balistik katsayı, kesitsel yoğunluğun (SD) merminin şekline bağlı form faktörüne (i) bölünmesi ile elde edilen sayıdır. Kesitsel yoğunluk (SD) ise merminin ağırlığının (M) çapının karesine (d2) bölünmesi ile elde edilir. Form faktörü de bazı formüllerle hesaplanabilirse de her zaman doğru sonuç vermeyebilir. Yivsiz tekkurşunlar için form faktörü genellikle 1 kabul edildiğinden BC=SD olur.
Balistik katsayı mesafe ve hız ile değişkenlik gösterdiğinden belirli mesafeye atış yaparak namlu çıkış hızı, menzildeki hızı ve mesafe üzerinden aşağıdaki formülle hesaplanabilir.
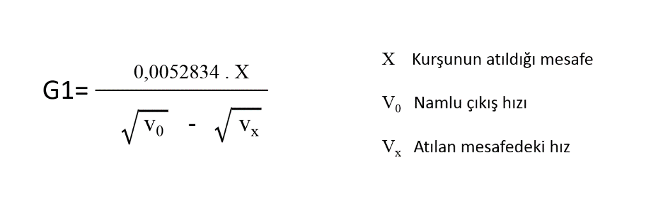
Pekiyi, bu hesaplamalar ne işe yarayacak derseniz balistik programlarda BC yi işleyerek, tek kurşunun hangi mesafede ne kadar düşüş yapacağını, enerjisinin ne olacağını ve ne zaman transsonik bölgeye girip dengesini ve isabetini kaybedeceğini bulabiliriz. Ben bunun için internette on-line olarak kullanılan başarılı bir programı tavsiye ederim: http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=de90a3b8
Transsonik etkileşim
Sesüstü hızda namludan çıkan mermi şiddetli ve artan bir hava direnci ile karşılaşarak yavaşlamaya başlıyor, şekilde izleyeceğiniz gibi mermi hızı ses hızına gelince aniden sürüklenme katsayısında (Drag) bir azalma oluyor, sürüklenme katsayısı süratle düşerken ses altı hıza ulaşınca hafif bir şekilde artış gösteriyor. İşte Mach 1.1 ile 0.8 hızları arasındaki bölgeye ( ortalama 1116 fps / 340 m/s) transsonik bölge adını veriyoruz.
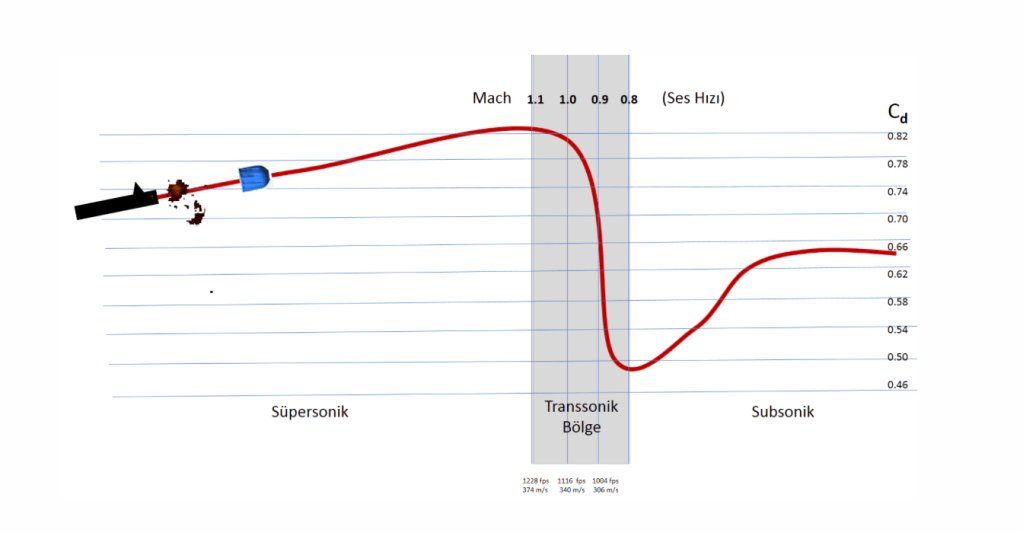
Mermi, bu bölgede sürüklenme katsayısının ani düşmesiyle, balistik değerlerinde, basınç merkezinde, ağırlık merkezindeki ani yer değiştirmeye bağlı olarak takla atabiliyor, az da olsa yön değiştirebiliyor. Transsonik bölgeye giren merminin nişan noktası (POA) ile vuruş noktası (POI) farklılaşıyor.Yivlilerde jiroskopik stabilite, hızlı çıkış ve yapısı nedeniyle ancak uzun mesafelerde gerçekleşirken, yivsizlerde namlu çıkış hızı daha düşük, balistik katsayı kötü, sadece çekme stabilitesi olduğu için kısa mesafelerde bu olay gerçekleşiyor. Yivizlerde 100 m içinde transsonik bölgeye girmeyecek 32 gram çekirdeğin hızının en az 487,5 m/s (1600 fps) hızda olması gerekiyor. Genellikle 1300 fps (396 m/s) civarında namlu çıkış hızındaki yivsiz tek kurşunlar balistik katsayısına da bağlı olarak genelde 30-40 metrede transsonik olup isabet kaybediyorlar.
Aşağıdaki resimde 36.5 metre (40 yarda) mesafede atılmış solda namlu çıkış hızı nedeniyle bu mesafede transsonik olmamış, sağda ise bu mesafe öncesinde transsonik bölgeye girmiş Foster tipi kurşunlarda isabeti görüyorsunuz.

Eğer namlu çıkış hızı 1050 fps (320 m/s) altındaki hızlarda subsonik mermi kullanırsak, transsonik etkilenme olmayacağından isabet yüksek olacaktır. Ancak hız azaldığı için enerjisi düşeceğinden büyük avlarda kullanılması pek tavsiye edilmemektedir. Yivsiz tüfeklerde subsonik fişek kullanımını ayrı bir konu başlığı halinde bu sitede bulabilirsiniz

